xxheexx

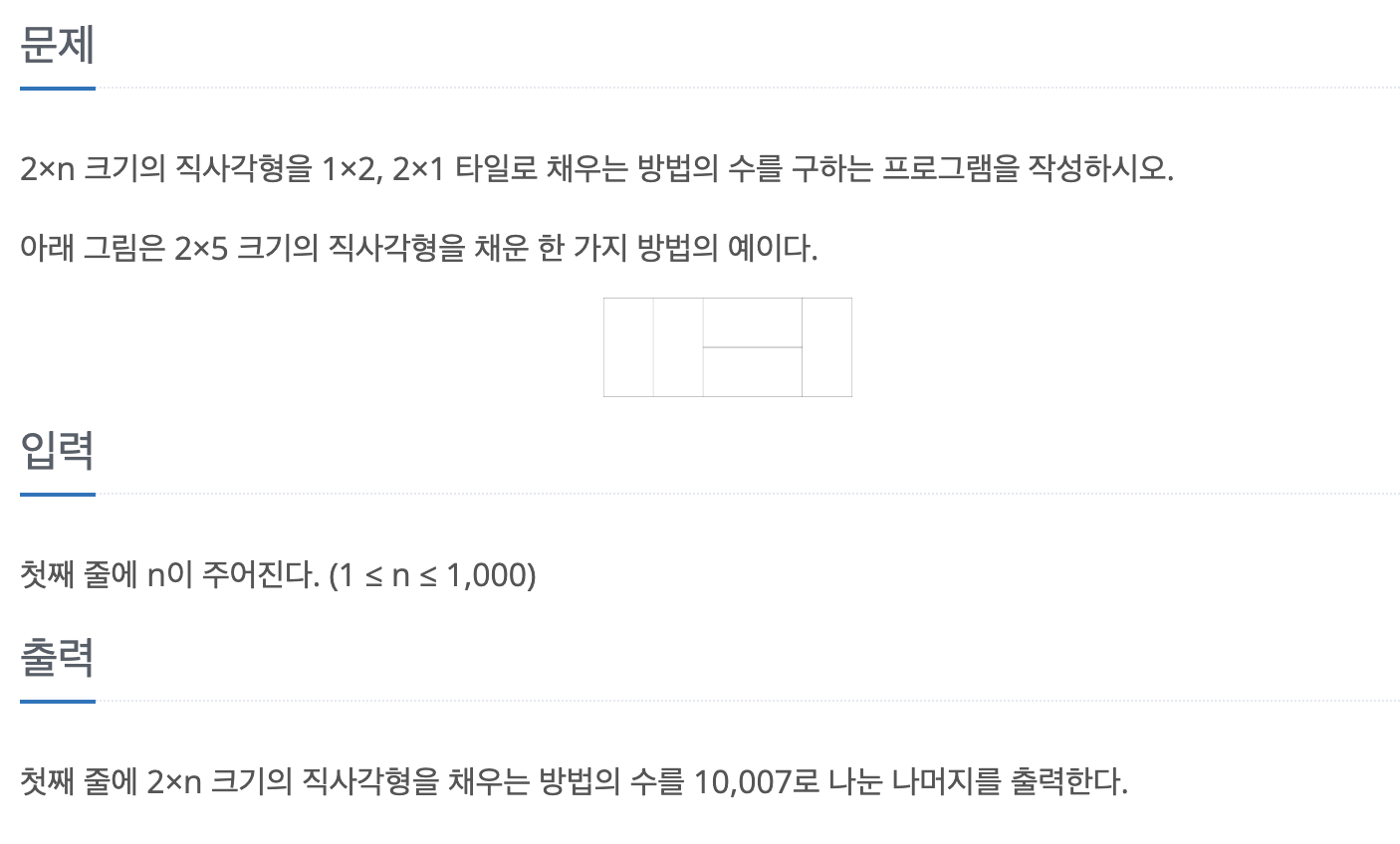
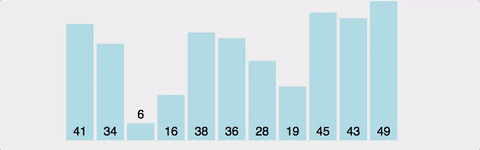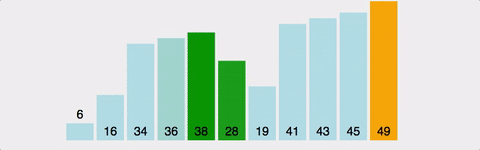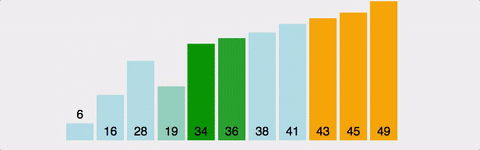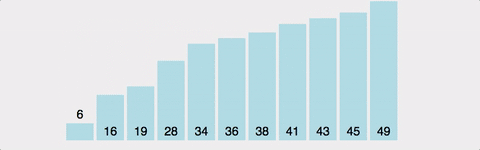
다이나믹 프로그래밍 여러 개의 하위 문제를 먼저 푼 후 그 결과를 쌓아올려 주어진 문제를 해결하는 알고리즘 문제를 해결하기 위한 점화식을 찾아낸 후 점화식의 항을 밑에서부터 차례로 구해나가서 답을 알아내는 형태 1. 테이블 정의하기 2. 점화식 찾기 3. 초기값 정하기 예제 - 백준 2 X n 타일링 (11726) #include using namespace std; int d[10005]; int mod = 10007; int main(void){ ios::sync_with_stdio(0); cin.tie(0); int n; cin >> n; d[1] = 1; d[2] = 2; for(int i = 3; i

상한 : 찾고자 하는 특정 값을 초과하는 '첫 위치' 반환 하한 : 찾고자 하는 특정 값 이상인 '첫 위치' 반환 -> 중복 값이 있을 때의 활용 arr1{1, 2, 2, 2, 3} 일 때 Key 값이 2이고, Upper Bound로 찾는다면 2를 초과되는 처음 위치인 arr[4] = 3인 index 4 반환 Lower Bound로 찾게 된다면 2 이상 위치 중 처음 위치인 arr[1] = 2인 index 1 반환 중복 원소에서 가장 끝 값(가장 오른쪽 값)을 찾고자 한다면 Upper Bound - 1 중복 원소 중 가장 왼쪽 끝 값(가장 왼쪽 값)을 찾고자 한다면 Lower Bound 그대로 private static int lowerBound(int[] arr, int key) { int lo = 0..

풀이 (참고) 길이에서 최대값(max)은 주어진 랜선의 길이중 최대값+1로 설정하고 최소값(min)은 0으로 시작한다. mid = (min+max)/2로 설정한 후 주어진 랜선의 길이에서 얻어낼 수 있는 랜선의 수 n을 구한다. n과 N을 비교해 n

완전탐색으로 구현 import java.util.*; import java.io.*; public class Main { static int N; static Vector v; static Stack st; static void print(){ if(st.size()==N) { for(int num:st){ System.out.print(num+" "); } System.out.println(); return; } for(int i=1;i

코드 import java.util.*; import java.io.*; class Solution { public String[] solution(String[] strings, int n) { String[] answer = {}; PriorityQueue pq = new PriorityQueue(); PriorityQueue stringspq = new PriorityQueue(); Vector v = new Vector(); Vector stringsv = new Vector(); for(int i=0;i

이분탐색 (Binary Search) 전체 범위를 이분할하여 가운데의 값을 비교하여 두 영역 중 다른 영역으로 이동하여 탐색 시간복잡도 : O(logN) 탐색 전 리스트가 반드시 정렬되어 있어야함 -> 배열을 적게 탐색하는 경우 이분탐색 쓰지 않는 것이 나을수도 있음 순차 탐색 vs 이분 탐색 정렬이 안되어있다면 상황에 따라 순차탐색이 더 나을 수도 있다 java public class BinarySearch { static int[] arr = {1, 3, 5, 7, 8, 10, 20, 35, 99, 100}; public static void main(String[] args) { System.out.println("1. 순환 호출을 이용한 이진 탐색"); System.out.println(binar..

map 활용 시 많이 쓰이는 함수 getOrDefault(Object key, V DefaultValue) 찾는 key가 존재하면 해당 key에 매핑되어 있는 값을 반환하고 그렇지 않으면 디폴트 값 반환 import java.util.HashMap; public class MapGetOrDefaultEx { public static void main(String arg[]) { String [] alphabet = { "A", "B", "C" ,"A"}; HashMap hm = new HashMap(); for(String key : alphabet) hm.put(key, hm.getOrDefault(key, 0) + 1); System.out.println("결과 : " + hm); // 결과 : {A..

import java.io.*; import java.util.*; class Solution { public int solution(String[] want, int[] number, String[] discount) { int answer = 0; Vector v = new Vector(); HashMap map = new HashMap(); HashMap sm = new HashMap(); for(int i=0;i

Sorting FIFO(First In, First Out) 구조 삽입과 삭제 연산이 서로 다른 한 군데 느린 알고리즘의 경우 시간복잡도가 O(N^2), 빠른경우 O(NlogN) 안정성이 보장되는 경우인지 판단해야함 안정성 보장 : 같은 키를 가진 데이터의 순서가 안 바뀜 1. 거품정렬 (Bubble Sort) 첫번째 원소부터 인접한 원소와 비교하며 자리를 바꾸며 맨 끝부터 정렬 가장 큰 값을 하나씩 뒤로 보내면서 뒤쪽부터 정렬 안정성 보장 O 시간 복잡도 : O(N^2) -> 비효율적 void bubble_sort(int list[], int n){ int i, j, temp; for(i=n-1; i>0; i--){ // 0 ~ (i-1)까지 반복 for(j=0; j

Brute Force 단순히 가능한 모든 경우 확인 테스트 케이스의 크기에 따라 소요 시간이 엄청나게 커질 수 있음 표본의 수와 시간복잡도 고려해 선택해야함 매직넘버 100,000,000 총 연산수가 약 1억회 이하 -> 충분히 완전탐색으로 접근 가능 대략적인 완전탐색 가능 기준으로 잡으면 유용 재귀함수 이용 Backtracking 완전탐색처럼 모든 경우를 탐색하나 중간 중간에 조건에 맞지 않는 케이스를 가지치기하여 탐색 시간 줄임 일반적으로 완전탐색에 비해 시간적으로 효율적 탐색 중 조건에 맞지 않는 경우 이전 과정으로 돌아가야하기 때문에 재귀 사용하는 경우 많음 조건을 어떻게 설정하고 틀렸을 시 어떤 시점으로 돌아가야할지 설계 잘해야함 예제 import java.io.*; import java.mat..